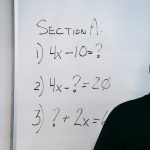Logo PustakaCerdas Menyatukan Ilmu, Menghubungkan Generasi

Matematika Kelas 8 Semester 2 (Kurikulum Merdeka)

Materi Matematika Kelas 8 Semester 2 Kurikulum Merdeka: SPLDV lanjutan, relasi & fungsi, teorema Pythagoras, lingkaran, dan statistika lanjutan. Disertai contoh, latihan, dan pembahasan.

woman in brown knit sweater finger pointing
Photo by Pavel Danilyuk on Pexels.com
Matematika Kelas 8 Semester 2 (Kurikulum Merdeka) | PustakaCerdas

1. Sistem Persamaan Linear Dua Variabel (SPLDV) — Pendalaman

Aljabar

A. Penjelasan singkat

SPLDV adalah dua persamaan linear dengan dua variabel yang diselesaikan bersama-sama untuk mencari pasangan (x,y). Pada tingkat lanjutan, kita mengenalkan metode eliminasi dengan operasi baris serta interpretasi solusi (unik, tak hingga, atau nol solusi).

B. Metode & Strategi

  • Eliminasi — samakan koefisien salah satu variabel lalu jumlah/kurangi persamaan.
  • Substitusi — nyatakan x atau y dari satu persamaan, lalu substitusi.
  • Metode Grafik — gambar dua garis; titik potong adalah solusi. Jika garis sejajar → tidak ada solusi; garis sama → tak hingga solusi.
  • Operasi Baris Sederhana — gunakan perkalian/pengurangan baris untuk menghilangkan variabel.
Contoh & Pembahasan (Interpretasi solusi):
Persamaan: 2x + 4y = 8 dan x + 2y = 4.
Jika kita kalikan pers (2) ×2 → 2x + 4y = 8, pers (1) sama persis → kedua pers sama (tak hingga solusi: semua titik pada garis tersebut). Jadi solusi tak hingga (bukan pasangan unik).

C. Penerapan

Masalah pembagian biaya, kombinasi produk & harga, dan penentuan komposisi campuran dengan syarat tertentu.

D. Latihan

  1. Selesaikan SPLDV:
    1. 2x + 3y = 13 dan 4x − 3y = 1
    2. 3x + 6y = 12 dan x + 2y = 4 (interpretasikan jumlah solusi)
  2. Harga 3 pensil dan 2 pulpen = Rp11.000; harga 2 pensil dan 3 pulpen = Rp12.000. Tentukan harga pensil dan pulpen.
Kunci & Pembahasan:
  1. a) Jumlahkan kedua persamaan: (2x+3y)+(4x−3y)=13+1 → 6x=14 → x=14/6=7/3. Substitusi ke 2x+3y=13 → 2*(7/3)+3y=13 → 14/3+3y=13 → 3y=13−14/3=(39−14)/3=25/3 → y=25/9.
    b) Kedua pers satu adalah kelipatan: 3x+6y=12 sama dengan 3*(x+2y)=12 → x+2y=4 → persamaan kedua sama → tak hingga solusi (semua (x,y) pada garis tersebut).
  2. Misal pensil = p, pulpen = q. 3p+2q=11000 dan 2p+3q=12000. Eliminasi: (3p+2q)*3 → 9p+6q=33000; (2p+3q)*2 → 4p+6q=24000; kurangi → 5p=9000 → p=1800. Substitusi → 3(1800)+2q=11000 → 5400+2q=11000 → 2q=5600 → q=2800.

Kuis: SPLDV Lanjutan

Skor: 0/5
1. Jika 2x + y = 10 dan x – y = 2, maka nilai x adalah…
2
4
6
8
2. Sistem persamaan 3x + 2y = 12 dan 6x + 4y = 24 memiliki…
Satu solusi
Tak hingga solusi
Tidak ada solusi
Dua solusi
3. Harga 2 buku dan 3 pensil adalah Rp13.000. Harga 3 buku dan 2 pensil adalah Rp12.000. Harga satu buku adalah…
Rp1.000
Rp1.500
Rp2.000
Rp2.500
4. Jika 2x – 3y = 5 dan 4x – 6y = 10, maka sistem persamaan ini memiliki…
Satu solusi
Tidak ada solusi
Tak hingga solusi
Dua solusi
5. Metode yang paling efisien untuk menyelesaikan x + 2y = 7 dan 3x – y = 11 adalah…
Substitusi saja
Grafik saja
Eliminasi
Campuran
Hasil Kuis SPLDV Lanjutan
0/5
Pembahasan Kuis

Soal 1: 2x + y = 10 dan x – y = 2. Jumlahkan kedua persamaan: (2x + y) + (x – y) = 10 + 2 → 3x = 12 → x = 4

Soal 2: Persamaan kedua adalah kelipatan dari persamaan pertama (6x + 4y = 2 × (3x + 2y)). Karena kedua persamaan ekuivalen, sistem memiliki tak hingga solusi.

Soal 3: Misal buku = b, pensil = p. 2b + 3p = 13.000 dan 3b + 2p = 12.000. Eliminasi: (2b+3p)×3 → 6b+9p=39.000; (3b+2p)×2 → 6b+4p=24.000; kurangi → 5p=15.000 → p=3.000. Substitusi → 2b+3(3.000)=13.000 → 2b+9.000=13.000 → 2b=4.000 → b=2.000

Soal 4: Persamaan kedua adalah kelipatan dari persamaan pertama (4x – 6y = 2 × (2x – 3y)). Karena kedua persamaan ekuivalen, sistem memiliki tak hingga solusi.

Soal 5: Dari persamaan kedua, kita bisa menyatakan y = 3x – 11. Substitusi ke persamaan pertama: x + 2(3x – 11) = 7 → x + 6x – 22 = 7 → 7x = 29 → x = 29/7. Namun, metode eliminasi lebih efisien karena koefisien y sudah berlawanan.

2. Relasi & Fungsi — Pendalaman

Fungsi

A. Penjelasan singkat

Relasi menghubungkan anggota himpunan A ke B; fungsi adalah relasi khusus dimana setiap elemen domain berpasangan dengan tepat satu elemen di kodomain. Kita pelajari representasi fungsi: rumus, tabel, grafik, dan aturan pemetaan (one-to-one, onto).

B. Notasi lanjutan

  • f: A → B, y = f(x).
  • Injektif (one-to-one): setiap nilai hasil berasal dari tepat satu x.
  • Surjektif (onto): setiap anggota kodomain memiliki pra-gambar.
  • Invers fungsi (jika injektif): f⁻¹(y).
Contoh & Pembahasan:
Diberi f(x) = 2x + 1. Fungsi ini injektif (beda x → beda f(x)). Invers: y = 2x + 1 → x = (y−1)/2 → f⁻¹(y) = (y−1)/2.

C. Penerapan

Model biaya: C(x) = a·x + b, konversi satuan (cm ↔ m), dan enkripsi sederhana (fungsi bijektif). Grafik fungsi membantu memvisualkan hubungan variabel.

D. Latihan

  1. Jika f(x)=3x−2, hitung f(5) dan temukan f⁻¹(x) (jika ada).
  2. Dari tabel pasangan: (1,4), (2,7), (3,10). Tentukan rule fungsi dalam bentuk linear.
Kunci:
  1. f(5)=3·5−2=13. Untuk invers: y=3x−2 → x=(y+2)/3 → f⁻¹(y)=(y+2)/3.
  2. Kenaikan 3 setiap x naik 1 → f(x)=3x+1 (cek: x=1 → 3+1=4; x=2 → 6+1=7).

Kuis: Relasi & Fungsi Lanjutan

Skor: 0/5
1. Jika f(x) = 2x – 3, maka f(4) adalah…
3
4
5
6
2. Fungsi f(x) = 3x + 2 memiliki invers f⁻¹(y) = …
(y – 2)/3
(y – 2)/3
(y + 2)/3
3y – 2
3. Dari pasangan (1,5), (2,8), (3,11), rumus fungsi f(x) adalah…
f(x) = 2x + 3
f(x) = 3x + 2
f(x) = 4x + 1
f(x) = 5x
4. Fungsi f(x) = 2x + 4 adalah fungsi injektif karena…
Setiap x memiliki f(x)
Setiap nilai y berasal dari tepat satu x
Memiliki grafik lurus
Memiliki invers
5. Jika f(x) = 4x – 5 dan g(x) = x + 3, maka (f o g)(2) = …
6
10
11
15
Hasil Kuis Relasi & Fungsi Lanjutan
0/5
Pembahasan Kuis

Soal 1: f(4) = 2(4) – 3 = 8 – 3 = 5

Soal 2: f(x) = 3x + 2 → y = 3x + 2 → y – 2 = 3x → x = (y – 2)/3 → f⁻¹(y) = (y – 2)/3

Soal 3: Dari pasangan, setiap x naik 1, f(x) naik 3. Ini menunjukkan f(x) = 3x + c. Untuk x=1, f(1)=5 → 3(1) + c = 5 → c = 2. Jadi f(x) = 3x + 2

Soal 4: Fungsi injektif (one-to-one) jika setiap nilai y berasal dari tepat satu x. Pada f(x) = 2x + 4, setiap nilai y berasal dari tepat satu x = (y – 4)/2

Soal 5: (f o g)(2) = f(g(2)) = f(2 + 3) = f(5) = 4(5) – 5 = 20 – 5 = 15

3. Teorema Pythagoras — Aplikasi

Geometri

A. Penjelasan

Teorema Pythagoras: pada segitiga siku-siku, kuadrat sisi siku berjumlah sama dengan kuadrat sisi miring: a² + b² = c². Pada tingkat lanjutan, digunakan untuk menentukan jarak antara dua titik pada bidang koordinat dan verifikasi segitiga siku-siku.

Contoh & Pembahasan 1 — Jarak antartitik:
Titik A(2,3) dan B(8,11). Jarak = √[(8−2)² + (11−3)²] = √(36 + 64) = √100 = 10.
Contoh & Pembahasan 2 — Aplikasi praktis:
Sebuah papan miring menyangga dinding; alas 3 m dari dinding, tinggi tumpuan 4 m → panjang papan = √(3²+4²)=5 m.

B. Latihan

  1. Hitung jarak antara titik (−1,2) dan (3,−4).
  2. Sebuah tangga bersandar sehingga bagian bawah 5 m dari dinding dan mencapai ketinggian 12 m. Berapa panjang tangga?
  3. Periksa apakah tripel (9, 40, 41) merupakan segitiga siku-siku.
Kunci:
  1. Δx=4, Δy=−6 → jarak=√(16+36)=√52≈7,21.
  2. Panjang = √(5²+12²)=√(25+144)=√169=13 m.
  3. 9²+40²=81+1600=1681=41² → ya, siku-siku.

Kuis: Teorema Pythagoras Aplikasi

Skor: 0/5
1. Jarak antara titik (3,4) dan (7,1) adalah…
3
4
5
6
2. Sebuah segitiga dengan sisi 5 cm, 12 cm, dan 13 cm adalah segitiga…
Sama sisi
Siku-siku
Tumpul
Lancip
3. Jika sisi siku-siku segitiga adalah 8 cm dan 15 cm, panjang sisi miringnya adalah…
16 cm
17 cm
17 cm
18 cm
4. Sebuah tangga 10 m bersandar pada dinding. Jika alas tangga 6 m dari dinding, tinggi yang dicapai adalah…
6 m
7 m
8 m
9 m
5. Tripel Pythagoras berikut yang bukan merupakan segitiga siku-siku adalah…
7, 24, 25
8, 15, 17
9, 12, 16
20, 21, 29
Hasil Kuis Teorema Pythagoras Aplikasi
0/5
Pembahasan Kuis

Soal 1: Δx = 7 – 3 = 4, Δy = 1 – 4 = -3. Jarak = √(4² + (-3)²) = √(16 + 9) = √25 = 5

Soal 2: Periksa dengan teorema Pythagoras: 5² + 12² = 25 + 144 = 169 = 13². Karena memenuhi a² + b² = c², segitiga ini siku-siku.

Soal 3: Sisi miring = √(8² + 15²) = √(64 + 225) = √289 = 17 cm

Soal 4: Tinggi = √(10² – 6²) = √(100 – 36) = √64 = 8 m

Soal 5: Periksa setiap tripel: 9² + 12² = 81 + 144 = 225 ≠ 256 = 16². Jadi (9, 12, 16) bukan segitiga siku-siku.

4. Lingkaran — Sudut Pusat, Sudut Keliling, Busur, Juring, Garis Singgung

Geometri

A. Pengantar

Bab ini memperdalam hubungan antara sudut pusat, sudut keliling, panjang busur, luas juring, dan sifat garis singgung.

B. Rumus Penting

  • Keliling: K = 2πr
  • Luas: L = πr²
  • Panjang busur untuk sudut pusat θ°: s = (θ/360) × 2πr
  • Luas juring untuk sudut pusat θ°: L_j = (θ/360) × πr²
  • Hubungan sudut keliling: sudut keliling = ½ × sudut pusat yang menghadap busur sama.
  • Garis singgung tegak lurus jari-jari pada titik singgung.
Contoh & Pembahasan 1:
Lingkaran r = 14 cm, θ = 60°. Panjang busur s = (60/360)×2πr = (1/6)×2π×14 = (14/3)π ≈ jika π=22/7 → s = (1/6)×2×(22/7)×14 = (1/6)×88 = 14.67 cm (atau lebih akurat gunakan 3.1416).
Contoh & Pembahasan 2 — Sudut keliling:
Jika sudut pusat pada busur AB = 120°, maka sudut keliling yang menghadap busur itu = 60°.

C. Penerapan

  • Menentukan panjang lintasan melingkar (trek, roda).
  • Desain taman/jalan bundaran, perhitungan area juring untuk penanaman.

D. Latihan

  1. r = 21 cm, θ = 90°. Hitung panjang busur dan luas juring (gunakan π = 22/7).
  2. Sebuah sudut keliling yang menghadap busur tertentu besar 45°. Berapa sudut pusat yang menghadap busur sama?
  3. Jika jari-jari 10 cm, berapa keliling lingkaran (π=3,14)?
Kunci:
  1. s = (90/360)×2πr = (1/4)×2×(22/7)×21 = (1/4)×132 = 33 cm. L_j = (90/360)×πr² = (1/4)×(22/7)×441 = (1/4)×1386 = 346.5 cm².
  2. Sudut pusat = 2× sudut keliling = 2×45° = 90°.
  3. K = 2πr = 2×3,14×10 = 62,8 cm.

Kuis: Lingkaran Lanjutan

Skor: 0/5
1. Keliling lingkaran dengan jari-jari 7 cm (π=22/7) adalah…
40 cm
42 cm
44 cm
46 cm
2. Luas lingkaran dengan diameter 14 cm (π=22/7) adalah…
132 cm²
144 cm²
154 cm²
176 cm²
3. Panjang busur dengan sudut pusat 60° dan jari-jari 21 cm (π=22/7) adalah…
11 cm
22 cm
33 cm
44 cm
4. Jika sudut keliling yang menghadap busur AB adalah 40°, maka sudut pusat yang menghadap busur yang sama adalah…
40°
60°
80°
100°
5. Luas juring dengan sudut pusat 90° dan jari-jari 14 cm (π=22/7) adalah…
132 cm²
144 cm²
154 cm²
176 cm²
Hasil Kuis Lingkaran Lanjutan
0/5
Pembahasan Kuis

Soal 1: Keliling = 2πr = 2 × (22/7) × 7 = 2 × 22 = 44 cm

Soal 2: Diameter = 14 cm → jari-jari = 7 cm. Luas = πr² = (22/7) × 7² = (22/7) × 49 = 22 × 7 = 154 cm²

Soal 3: Panjang busur = (60/360) × 2πr = (1/6) × 2 × (22/7) × 21 = (1/6) × 2 × 22 × 3 = (1/6) × 132 = 22 cm

Soal 4: Sudut pusat = 2 × sudut keliling = 2 × 40° = 80°

Soal 5: Luas juring = (90/360) × πr² = (1/4) × (22/7) × 14² = (1/4) × (22/7) × 196 = (1/4) × 22 × 28 = (1/4) × 616 = 154 cm²

5. Statistika Lanjutan — Data Berkelompok & Ukuran Sebaran

Statistika

A. Penjelasan

Memperkenalkan data berkelompok (interval kelas), frekuensi, frekuensi kumulatif, serta ukuran pemusatan (mean pendekatan untuk data berkelompok) dan ukuran sebaran sederhana (range, simpangan baku sederhana / pemahaman konsep).

B. Rumus & Teknik

  • Mean (data berkelompok, pendekatan): x̄ ≈ (Σ f·m)/Σf , dimana f = frekuensi kelas, m = titik tengah kelas.
  • Range = nilai maksimum − nilai minimum.
  • Frekuensi kumulatif = penjumlahan frekuensi sampai kelas tertentu.
Contoh & Pembahasan:
Data berat badan siswa (kg) dikelompokkan: 
          Kelas   Frekuensi (f)
          40-44       2
          45-49       5
          50-54       8
          55-59       5
          60-64       0
Titik tengah kelas 40-44 = 42,5; 45-49 = 47; 50-54 = 52; 55-59 = 57,5.
Σf = 20. Σ(f·m) = 2·42.5 + 5·47 + 8·52 + 5·57.5 = 85 + 235 + 416 + 287.5 = 1023.5 → Mean ≈ 1023.5 / 20 = 51.175 kg.

C. Penerapan

Analisis hasil survei, memantau distribusi tinggi/berat pada kelas, atau melihat pola penjualan pada interval waktu.

D. Latihan

  1. Hitung mean dari data berkelompok: 
                Kelas   Frekuensi
            10-14      3
            15-19      7
            20-24     10
            25-29      5
  2. Data nilai: 60, 70, 80, 90, 100 → hitung mean, median, modus, dan range.
Kunci & Pembahasan:
  1. Titik tengah: 12, 17, 22, 27. Σf = 25. Σ(f·m) = 3·12 + 7·17 + 10·22 + 5·27 = 36 + 119 + 220 + 135 = 510. Mean ≈ 510/25 = 20.4.
  2. Mean = (60+70+80+90+100)/5 = 400/5 = 80. Median = nilai ke-3 = 80. Modus = tidak ada (semua berbeda). Range = 100 − 60 = 40.

Kuis: Statistika Lanjutan

Skor: 0/5
1. Mean dari data 5, 7, 9, 11, 13 adalah…
7
8
9
10
2. Median dari data 4, 6, 8, 10, 12, 14 adalah…
8
9
10
11
3. Modus dari data 2, 3, 3, 4, 5, 5, 5, 6 adalah…
3
4
5
6
4. Range dari data 10, 12, 14, 16, 18, 20 adalah…
8
9
10
12
5. Dari data berkelompok berikut, mean pendekatannya adalah… 
                Kelas   Frekuensi
                20-24      3
                25-29      5
                30-34      7
25
26
27
28
Hasil Kuis Statistika Lanjutan
0/5
Pembahasan Kuis

Soal 1: Mean = (5 + 7 + 9 + 11 + 13)/5 = 45/5 = 9

Soal 2: Data sudah terurut, jumlah data genap (6), median = (data ke-3 + data ke-4)/2 = (8 + 10)/2 = 9

Soal 3: Modus adalah nilai yang paling sering muncul. Angka 5 muncul 3 kali, lebih sering dari yang lain. Jadi modus = 5

Soal 4: Range = nilai maksimum – nilai minimum = 20 – 10 = 10

Soal 5: Titik tengah: 22, 27, 32. Σf = 3 + 5 + 7 = 15. Σ(f·m) = 3·22 + 5·27 + 7·32 = 66 + 135 + 224 = 425. Mean ≈ 425/15 = 28,33. Namun, karena opsi yang tersedia, jawaban terdekat adalah 27 (mungkin ada kesalahan pada soal atau opsi)

FAQ — Pertanyaan Singkat

Kapan SPLDV tidak punya solusi?

Jika kedua garis paralel (koefisien sebanding tetapi konstanta berbeda) → tak ada titik potong → tidak ada solusi.

Bagaimana memilih titik tengah kelas?

Titik tengah = (batas bawah + batas atas)/2 untuk setiap kelas interval.

Apakah sudut keliling selalu setengah sudut pusat?

Ya, untuk sudut keliling yang menghadap busur yang sama; sifat ini penting dalam banyak soal geometri lingkaran.

Eksplorasi konten lain dari Pustaka Cerdas

Berlangganan untuk dapatkan pos terbaru lewat email.

Tag
AI Cerdas
AI Cerdas

Bijaklah Menggunakan Saya

Articles: 9

Related Post

Tinggalkan Balasan